# Set Theory Axioms

Specifically, ZFC is a collection of approximately 9 axioms (depending on convention and precise formulation) that, taken together, define the core of mathematics through the usage of set theory. More formally, ZFC is a predicate logic equipped with a binary relation ∈, which refers to set membership and is read as "in". To be clear, it is said that a∈b when a is an element of b.

# Notation

In general, statements in set theory are expressed using first-order logic, which uses a number of quantifiers (or logical symbols):

means "is in", as in the introduction.
means "for all"; e.g. (translated: for all real ) is a way of expressing the trivial inequality.
means "there exists"; e.g. (translated: for all real , there exists a real such that y^3=x) is a way of stating that every real number has a real cube root.
means "is equivalent to". For example, is a way of expressing the fact that is positive if and only if is positive.
means "implies". For example, s a way of expressing the fact that the square of a positive number is positive. Note that , since is a false statement (e.g. for ).
means "logical and"; e.g. is a way of expressing the fact that is positive and is negative; i.e. is negative.

This allows for the axioms in ZFC to be stated succinctly using symbols, as in the following section.

# Formal Definition (Axioms)

The axioms of ZFC can be stated in several equivalent ways, and have slightly different names and logical formulations depending on the source. Of course, each individual source will have a rigorous correct treatment of the axioms, one of which follows:

# Axiom of extensionality

TIP

In other words, if for all , then . In plain language, this statement is equivalent to "If two sets have the same elements, they are the same set."

# Axiom of pairing

where

denotes the logical or quantifier.

TIP

In other words, for all and , there exists a such that for all , is equivalent to the statement " or ". In plain language, this statement is equivalent to "Given two elements, there exists a set containing exactly those two elements."

# Axiom of comprehension

$ϕ$

where

is the logical and quantifier, and

is an arbitrary property.

Axiom of comprehension

Axiom of comprehension: the elements of satisfying form a new set

TIP

In plain language, this statement is equivalent to "Given any property and set , there exists a set containing all elements of that satisfy ." In informal terms, a subset of a set can be constructed by a succinct rule; e.g. the rule " even" applied to the set of integers results in a new set.

# Axiom of union

where

is the logical and qualifier.

TIP

In other words, for all there exists a such that for all , is equivalent to the statement "There exists such that and ." In plain language, there exists a set consisting of the union of all elements of .

# Axiom of power set

TIP

In other words, for any set , there exists a set whose elements are subsets of . In plain language, this axiom states that the power set of exists.

# Axiom of infinity

TIP

In simpler terms, an infinite set exists.

# Axiom of replacement

If is any function, then for any set there exists a set . The statement in logical quantifiers is more complex.

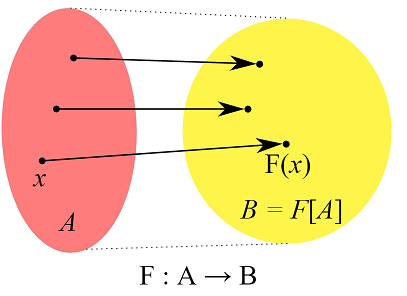
Axiom of replacement

A function takes any set to a new set

# Axiom of regularity

TIP

In other words, for all non-empty sets , there exists an element of that is disjoint with (shares no elements with ). This has two major consequences:

No set can be an element of itself. This resolves Russell's paradox.
Every set has a smallest element with respect to ∈.

These 8 axioms define a consistent theory, ZF (though, of course, it is very difficult to prove that this system is consistent). When the axiom of choice is added to the eight axioms above, the theory becomes ZFC (the "C" for choice), and it is this system that is commonly used as the foundation of mathematics.

← Tallteori, Pytagoreiske tripler. Functions →